lin_alg.h File Reference

Linear algebra functions. More...

#include "matpackI.h"

Include dependency graph for lin_alg.h:

This graph shows which files directly or indirectly include this file:

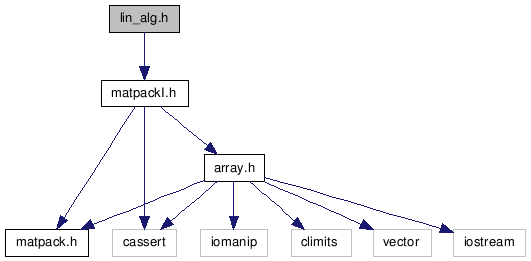
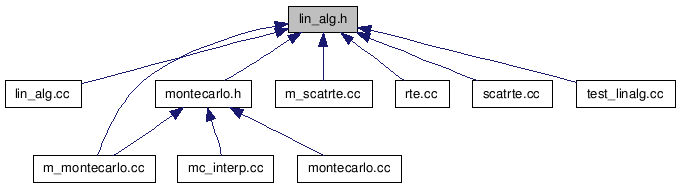
Go to the source code of this file.

Functions
void	ludcmp (MatrixView LU, ArrayOfIndex &indx, ConstMatrixView A)
	LU decomposition.
void	lubacksub (VectorView x, ConstMatrixView LU, ConstVectorView b, const ArrayOfIndex &indx)
	LU backsubstitution.
void	matrix_exp (MatrixView F, ConstMatrixView A, const Index &q)
	Exponential of a Matrix.
Numeric	norm_inf (ConstMatrixView A)
	Maximum absolute row sum norm.
void	id_mat (MatrixView I)
	Identity Matrix.

---

Detailed Description

Linear algebra functions.

Author:

Claudia Emde <claudia.emde@dlr.de>

Date:

Thu May 2 14:34:05 2002

Definition in file lin_alg.h.

---

Function Documentation

void id_mat

(

MatrixView

I

)

Identity Matrix.

Parameters:

I

Output: identity matrix

Definition at line 298 of file lin_alg.cc.

References ConstMatrixView::ncols(), and ConstMatrixView::nrows().

Referenced by include_cumtrans_in_diy_dq(), matrix_exp(), MCGeneral(), MCIPA(), mcPathTrace(), mcPathTraceGeneral(), mcPathTraceIPA(), and rte_step_std().

void lubacksub	(	VectorView	x,
		ConstMatrixView	LU,
		ConstVectorView	b,
		const ArrayOfIndex &	indx
	)

LU backsubstitution.

Solves a set of linear equations Ax=b. It is neccessairy to do a LU decomposition using the function ludcp before using this function.

Parameters:

	x	Output: Solution vector of the equation system.
	LU	Input: LU decomposition of the matrix (output of function ludcp).
	b	Input: Right-hand-side vector of equation system.
	indx	Input: Pivoting information (output of function ludcp).

Definition at line 144 of file lin_alg.cc.

References is_size(), and ConstMatrixView::nrows().

Referenced by matrix_exp(), rte_step_std(), test_lusolve1D(), and test_lusolve4D().

void ludcmp	(	MatrixView	LU,
		ArrayOfIndex &	indx,
		ConstMatrixView	A
	)

LU decomposition.

This function performes a LU Decomposition of the matrix A. (Compare Numerical Recipies in C, pages 36-48.)

Parameters:

	LU	Output: returns L and U in one matrix
	indx	Output: Vector that records the row permutation.
	A	Input: Matrix for which the LU decomposition is performed

Definition at line 53 of file lin_alg.cc.

References abs, is_size(), ConstMatrixView::nrows(), and temp.

Referenced by matrix_exp(), rte_step_std(), test_lusolve1D(), and test_lusolve4D().

void matrix_exp	(	MatrixView	F,
		ConstMatrixView	A,
		const Index &	q
	)

Exponential of a Matrix.

The exponential of a matrix is computed using the Pade-Approximation. The method is decribed in: Golub, G. H. and C. F. Van Loan, Matrix Computation, p. 384, Johns Hopkins University Press, 1983.

Parameters:

	F	Output: The matrix exponential of A (Has to be initialized before calling the function.
	A	Input: arbitrary square matrix
	q	Input: Parameter for the accuracy of the computation

Definition at line 193 of file lin_alg.cc.

References id_mat(), is_size(), joker, lubacksub(), ludcmp(), mult(), N, ConstMatrixView::ncols(), and norm_inf().

Referenced by rte_step_std(), test_matrix_exp1D(), test_matrix_exp3D(), and test_matrix_exp4D().

Numeric norm_inf

(

ConstMatrixView

A

)

Maximum absolute row sum norm.

This function returns the maximum absolute row sum norm of a matrix A (see user guide for the definition).

Parameters:

A

Input: arbitrary matrix

Returns:

Maximum absolute row sum norm

Definition at line 275 of file lin_alg.cc.

References abs, ConstMatrixView::ncols(), norm_inf(), and ConstMatrixView::nrows().

Referenced by matrix_exp(), and norm_inf().