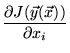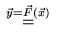Adjoint Models
Christian Melsheimer
IUP, University of Bremen
4th International Radiative Transfer Modeling Workshop, Bredbeck, 9 July, 2002
Let < u, v > be some scalar product, L some linear
operator1.
Then the adjoint operator L * defined by
< u, L * v > = < Lu, v >
If L is a real matrix, then
L * = LT (transpose); if L is a
complex matrix, then
L * = 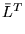 (complex conjugate,
transpose).
(complex conjugate,
transpose).
where
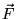
- is a complicated, non-linear, nasty function (``the
Model'');
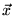
- is the model input (often the retrieval
variable);
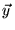
- is the model output (simulated measurement).
where 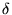 x is a small disturbance;
x is a small disturbance;
or, the other way round:
where 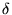 y is a small disturbance;
y is a small disturbance;
or even:
where
J(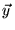 (
(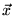 )) is, e.g., a cost function, a measure for
some error of
)) is, e.g., a cost function, a measure for
some error of
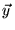 (
(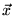 ) with respect to the measurement
) with respect to the measurement
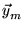 .
.
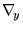 and
and
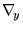 are the gradients with
respect to
are the gradients with
respect to 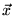 and
and 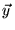 , respectively.
, respectively.
where K is the Jacobian of 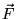 !
!
Here we have a linear mapping from 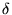 y to
y to 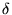 x that
involves the first derivative (something like a tangent) of the forward model, hence
the name ``tangent-linear''.
x that
involves the first derivative (something like a tangent) of the forward model, hence
the name ``tangent-linear''.
where KT is the adjoint of K, i.e. the adjoint of the tangent
linear model, hence the name. It is usually just called ``adjoint
model'', although the correct name is ``adjoint tangent-linear model''.
If:
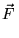
(
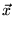
) =
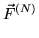
(...(
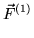
(
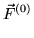
(
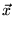
))..) (a sequence of operations)
then:
K = K(N) ... K(1)K(0)
and:
KT = K(0)TK(1)T ... K(N)T
- Adjoint models are widely used in meteorology, particularly for
assimilation schemes
- ECMWF, MétéoFrance and others have adopted official coding
conventions for adjoint models
- There are adjoint model compilers (at least in FORTRAN77) to
automatically generate the code for the adjoint model from the code
for the forward model, e.g. TAMC (Tangent Linear and Adjoint Model
Compiler) by Ralf Giering (see below)
BUT:
- How to apply adjoint models to the actual retrieval in
atmospheric sounding (OEM, Levenberg-Marquardt etc.)?
- Would it really make things easier (we still need the Jacobian ...)?
[...]
- Errico, R.M.: What is an adjoint model?
Bull. Am. Met. Soc., vol. 78, p. 2577, 1997.
- Rodgers, C.D.: Inverse Methods for Atmospheric
Sounding: Theory and Practice,
238 pp., World Scientific, Singapore, 2000. ISBN 981-02-2740-X
- Giering, R.: Automatic Adjoint and Tangent Linear Code
Generation,
http://www.npaci.edu/Research/ESS/seminars/giering.htm
- Kornblueh, L., Working group on Model evaluation and data
assimilation, Technical Explanations,
http://www.mpimet.mpg.de/working_groups/wg3/node3.html
Adjoint Models
This document was generated using the
LaTeX2HTML translator Version 2002 (1.64)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -html_version 4.0,math -nomath -noascii_mode -nonavigation adjoint_models.tex
The translation was initiated by Christian Melsheimer on 2002-08-01
Footnotes
- ...
operator1
- The usual conditions apply, such as u
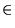 vector
space U and v
vector
space U and v 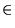 vector space V etc.
vector space V etc.
Christian Melsheimer
2002-08-01
![]() (complex conjugate,
transpose).
(complex conjugate,
transpose).
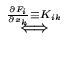
![]() y to
y to ![]() x that
involves the first derivative (something like a tangent) of the forward model, hence
the name ``tangent-linear''.
x that
involves the first derivative (something like a tangent) of the forward model, hence
the name ``tangent-linear''.